"Кенгуру" 2011 - 7-8 класс, задания и ответы

Приближается международный математический конкурс «Кенгуру».
Предлагаем вам задания и ответы на «Кенгуру» для 7-8 классов 2011 года.
Ответы находятся внизу страницы, после заданий и перед комментариями.

Задачи, оцениваемые в 3 балла

1. Электронные часы показывают 20:11. Сколько минут пройдет прежде, чем часы впервые покажут тот же набор цифр 0, 1, 1 и 2 в некотором другом порядке?
Варианты:
(А) 45 (Б) 49 (В) 50 (Г) 59 (Д) 60

2. На рисунке изображены три квадрата с общим центром. Площадь самого маленького квадрата равна 6. Чему равна площадь закрашенной области?

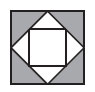
Варианты:
(А) 6 (Б) 12 (В) 15 (Г) 18 (Д) 24

3. На одной стороне улицы стоят дома с четными номерами: 2, 4, 6 а
на другой стороне — с нечетными: 1, 3, 5, ... Последний дом на четной стороне имеет номер 12, а всего на улице 17 домов. Какой номер имеет последний дом на нечетной стороне?
Варианты:
(А) 5 (Б) 7 (В) 13 (Г) 17 (Д) 21

4. Значение выражения 2011*2,011/201,1*20,11 равно
Варианты:
(А) 0,01 (Б) 0,1 (В)1 (Г) 10 (Д) 100

5. Из всех трехзначных чисел, сумма цифр которых равна 8, выбрали самое маленькое и самое большое. Чему равна их сумма?
Варианты:
(А) 707 (Б) 907 (В) 916 (Г) 1000 (Д) 1001

6. Среднее арифметическое чисел а и b равно 17, а среднее арифметическое чисел а, b и с равно 15. Чему равно с?
Варианты:
(А) 14 (Б) 13 (В) 12 (Г) 11 (Д)10

8. Чему равно (a:b):(с:d)?
Варианты:
(A) ad/bc (Б) ac/bd (В) ab/cd (Г) bc/ad (Д) cd/ab

9. Когда от каждого из двух чисел отняли половину меньшего из них, оказалось, что большая разность в три раза больше меньшей. Во сколько раз большее число больше меньшего?
Варианты:
(А)1 (Б) 2 (В)3 (Г) 4 (Д)5

10. Сколькими способами к фигуре на рисунке можно добавить одну клетку так, чтобы получившаяся фигура имела ось симметрии?

Варианты:
(А)1 (Б) 2 (В)3 (Г) 4 (Д)5

Задачи, оцениваемые в 4 балла

11. Положительное число а меньше 1, а число b больше 1. Какое из следующих чисел наибольшее?
Варианты:
(A) a+b (Б) ab (В)a/b (Г) b (Д) невозможно определить

12. Каждую область на рисунке надо покрасить в один из четырех цветов: красный (К), зеленый (3), синий (С) или желтый (Ж). Любые две области, имеющие общую границу, должны быть покрашены в разные цвета. Три области уже покрашены. Каким цветом будет покрашена область, отмеченная буквой X?

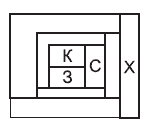
Варианты:
(А) красным (Б) синим (В) зеленым (Д) невозможно определить

13. Дима ввел новую операцию: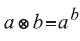
Если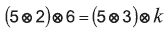
то k равно
Варианты:
(А) 3 (Б) 4 (В) 6 (Г) 8 (Д)12

14. Квадратный лист бумаги разделен на 6 прямоугольников (см. рисунок). Сумма периметров всех шести прямоугольников равна 120. Чему равна площадь этого листа бумаги?

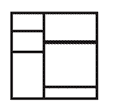
Варианты:
(А) 48 (Б) 64 (В) 110,25 (Г) 144 (Д) 256

15. Каждый год в день конкурса «Кенгуру» Вася несется в школу из дома бегом. В этом году ему понадобилось на дорогу на 20% меньше времени, чем в прошлом. Это значит, что его скорость возросла на
Варианты:
(А) 10% (Б) 20% (В) 25% (Г) 50% (Д) 100%

16.

17.       Сторона клетки на рисунке равна 1. Сколько существует ломаных длины 5, идущих по сторонам клеток, начинающихся в узле и содержащих точки А и В?

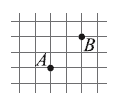
Варианты:
(А) 12 (Б) 24 (В) 30 (Г) 36 (Д) 54


18.       Маша выписала в ряд числа от 1 до 100, подчеркнула некоторые цифры, а потом переписала все подчеркнутые цифры в том же порядке без пробелов. Она получила строчку 20112011..., состоящую из нескольких «экземпляров» числа 2011. Какое наибольшее число этих экземпляров могло получиться?
Варианты:
(А) 2 (Б)3     (В) 4    (Г) 5    (Д)6

19. Замкнутая ломаная на поверхности куба проходит через две вершины и середины двух ребер (см. рисунок). Как может выглядеть развертка этого куба?

Варианты:

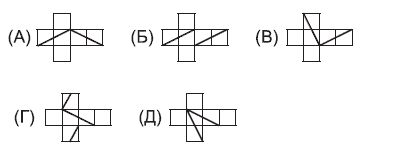
20. По кругу пишут 6 различных чисел так, чтобы любые два соседних числа отличались на 3 или на 5. Какова наибольшая возможная разность между двумя из написанных чисел?
Варианты:
(А) 15 (Б) 13 (В) 11 (Г) 5 (Д) 3

Задачи, оцениваемые в 5 баллов

21. На плоскости нарисован отрезок АВ длины 4. Сколько существует точек С таких, что треугольник ABC прямоугольный и его площадь равна 1?
Варианты:
(А) 2 (Б) 4 (В) 6 (Г) 8 (Д) Ю

22. Какое наименьшее целое значение может принимать выражение K*A*N*G*A*R*O*O/ G*A*M*E , если разными буквами обозначены различные
ненулевые цифры, а одинаковыми буквами — одинаковые цифры?
Варианты:
(А) 1 (Б) 2 (В)3 (Г) 5 (Д)7

23. Из двух диаметрально противоположных точек кругового трека одновременно стартуют два велосипедиста. Они едут в одном направлении с постоянными скоростями. Время от времени первый велосипедист обгоняет второго. Третий обгон произошел через 1 час после начала движения. Через сколько минут после третьего случится четвертый обгон?
Варианты:
(А) 6 (Б) 12 (В) 15 (Г) 20 (Д) 24

24. Каждый угол k-угольника равен 90° или 150°. Чему может быть равно k?
Варианты:
(А) 5 (Б) 8 (В) 9 (Г) 13 (Д) 14

25. Дрозды Алекс, Макс и Оскар построили гнезда. Алекс сказал: «От Макса я более чем в два раза дальше, чем от Оскара». Макс сказал: «От Оскара я более чем в два раза дальше, чем от Алекса». Оскар сказал: «От Макса я более чем в два раза дальше, чем от Алекса». Двое из них точно сказали правду. Кто ошибся?
Варианты:
(А) Макс (Б) Алекс (В) Оскар (Г) никто (Д) невозможно определить

26. На листе бумаги изображены четыре прямые l1, l2, l3 и l4 . Вася добавил к рисунку оси координат и вычислил угловые коэффициенты этих прямых: k1, k2, k3 и k4 соответственно. Какое из неравенств точно не будет выполняться?

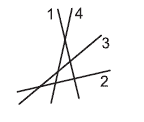
Варианты:
(А) k1<k2<k3<k4 (Б) k4<k1<k2<k3 (В) k3<k4<k1<k2 (Г) k2<k3<k4<k1 (Д) k2<k4<k3<k1

27. Требуется вписать числа 1, 2, 3, 4, 6, 8 и 9 в кружки так, чтобы произведения чисел на каждой из трех линий были одинаковыми. Какое число окажется в закрашенном кружке?

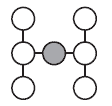
Варианты:
(А) 1 (Б) 2 (В) 6 (Г) 8 (Д)9

28. В треугольнике ABC сумма сторон АВ и АС равна 10, а угол ВАС равен 30°. Из вершины А проведены высота h, биссектриса l и медиана m. Какое из утверждений А — Г может быть неверным?
Варианты:
(A) h < 5 (Б) m < 5 (В) периметр треугольника не больше 20 (Г) l > 0,5 (Д) все утверждения А — Г обязательно выполняются

29. Сейчас произведение возрастов черепах Чапы и Паши равно 2³ * З³ * 11. Через год произведение их возрастов наверняка не будет делиться на
Варианты:
(А) 7 (Б) 15 (В) 18 (Г) 22 (Д) 55

30.