Представляем вниманию школьников 9-10 классов и их родителей возможность сверить свои задания с ответами к конкурсу «Кенгуру».
Вопросы сгруппированы по сложности (по баллам). Ответы на задания находятся после вопросов.

Задачи, оцениваемые в 3 балла

1. Бабочку отразили зеркально относительно прямой b, а потом повернули на 90° против часовой стрелки вокруг кончика носа кенгуру (точки А). После этого бабочка оказалась у кенгуру

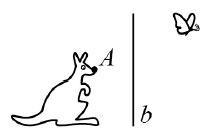
Варианты:
(А) на носу (Б) на лапе (В) на хвосте (Г) на спине (Д) в сумке

 
2. Сумма цифр семизначного числа равна 6. Чему равно произведение цифр этого числа?
Варианты:
(А) 0  (Б) 5  (В) 6  (Г) 7  (Д) невозможно определить

4. Сколько копеек в децисантикилорубле?
Варианты:
(А) 0,1              (Б) 1  (В) 10   (Г) 100  (Д) 1000

 
5. В Венеции каждый день происходит небольшое наводнение: вода поднимается, а потом отступает. На графике показано изменение уровня воды 6 мая 2011 года. Сколько часов в этот день уровень воды был выше 30 см?

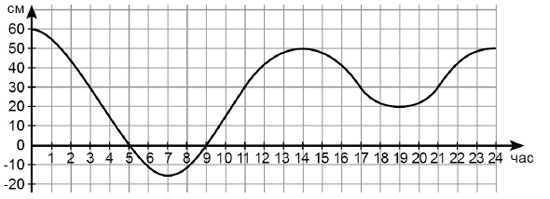
Варианты:
(А) 5   (Б) 6    (В) 7    (Г) 9    (Д) 12

6.         Число, куб которого равен 2012¹², умножили на квадрат числа 2012¹¹. Что получилось?
Варианты:
(А) 2012 ²¹ (Б) 2012 ²⁶ (В) 2012 ³¹ (Г) 2012 ⁵⁸ (Д) 2012 ⁸⁸

7.         Жук Жак ползёт по координатной плоскости. Он стартует из точки (1; 1) и движется так, что произведение его координат не меняется. По какой линии ползёт жук?
Варианты:
(А) по прямой (Б) по окружности  (В) по параболе  (Г) по гиперболе (Д) по ломаной линии

8.         Часы лежат на столе циферблатом вверх. Минутная стрелка сейчас указывает на юго-восток. Через сколько минут она будет указывать на северо-восток?
Варианты:
(А) 15 (Б) 20  (В) 30  (Г) 40  (Д) 45

9.         Как гласит русская поговорка, ложка дёгтя портит бочку мёда. Сколько банок мёда удастся испортить десятью каплями дёгтя, если в бочке 40 банок, а в ложке 200 капель?
Варианты:
(А) 2   (Б) 4    (В) 5    (Г) 10   (Д) 20

10.       Про число х известно, что х³<64<х² . Тогда
Варианты:
(А) 0<х<64     (Б) -8<х<4      (В)-4<х<8   (Г) х < -8 (Д) такого числа х не существует

Задачи, оцениваемые в 4 балла

11.       Фигура на рисунке образована двумя квадратами, треугольником, площадь которого равна 8 см² , и закрашенным параллелограммом. Чему равна площадь этого параллелограмма?

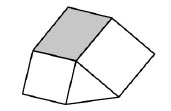
Варианты:
(А) 15 см² (Б) 16 см² (В) 18 см² (Г) 20 см² (Д) 21 см²

12.       Маша изучает натуральные числа, которые делятся на 72 и имеют в своей десятичной записи только нули и единицы. Сколько цифр в самом маленьком из таких чисел?
Варианты:
(А) 9   (Б) 11  (В) 12  (Г) 13  (Д) 14

13.       В семье пятеро мужчин: Иван Сидорович, Сидор Иванович, Сидор Петрович, Пётр Сидорович и Пётр Петрович. Один из них сейчас смотрит в окно, его отец спит, брат читает книгу, а сыновья ушли гулять. Как зовут того, кто смотрит в окно?
Варианты:
(А) Иван Сидорович
(Б) Сидор Иванович
(В) Сидор Петрович
(Г) Пётр Сидорович
(Д) Пётр Петрович

14.       Две стороны четырёхугольника равны 1 и 7. Одна из диагоналей, длина которой равна 3, делит его на два равнобедренных треугольника. Чему равен периметр этого четырёхугольника?
Варианты:
(А) 12 (Б) 14  (В) 16  (Г) 18  (Д) 20

15.       Натуральные числа а и b таковы, что a + b = 2012. Какое из следующих равенств возможно при некотором натуральном k ?
Варианты:

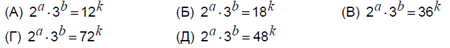
16.       Число х отрицательно, а число у положительно. Что не может произойти, если х увеличить, а у — уменьшить?
Варианты:
(А) х + у увеличится (Б) x/y уменьшится (В) y/x уменьшится  (Г) у — х уменьшится (Д) x-y уменьшится

17.       На какое наименьшее число тупоугольных треугольников можно разрезать квадрат?
Варианты:
(А) 4 (Б) 5 (В) 6 (Г) 7            (Д) это невозможно сделать

18.       Какое из утверждений А-Г неверно?
Варианты:
(A)      произведение любых двух нечётных чисел — нечётное число
(Б) произведение любых двух нечётных функций — нечётная функция
(B)       произведение любых двух чётных чисел — чётное число
(Г) произведение любых двух чётных функций — чётная функция
(Д) все утверждения А-Г верны

19.       В некоторых клетках таблицы 10x10 поставлены крестики так, что каждый из них — единственный либо в своей строке, либо в своём столбце. Какое наибольшее число крестиков может быть в такой таблице?
Варианты:
(А) 10 (Б) 15  (В) 18  (Г) 19  (Д) 99

20.       Разность корней квадратного уравнения х² + bх + с = 0 — чётное число. Чему может равняться ордината вершины параболы у = х² +bx + c ?
Варианты:
(А)-2   (Б) -3   (В)-4   (Г) -5   (Д)-6

Задачи, оцениваемые в 5 баллов

21. Винни-Пух пошёл в магазин за мёдом. Цена одного горшочка — 1 фунт, но при покупке n горшочков (n<100 ) покупатель получает скидку n %. Когда Винни вернулся домой, Кристофер Робин посмотрел на его покупку и сказал: «Глупенький мой мишка! Ты ухитрился заплатить за мёд наибольшую возможную сумму денег!». Сколько фунтов заплатил Винни-Пух?
Варианты:
(А) 10 (Б) 15 (В) 20 (Г) 25 (Д) 50

22. Числа от 1 до 120 выписаны в 15 строк, как показано на рисунке. В каком из столбцов (считая слева) сумма чисел самая большая?

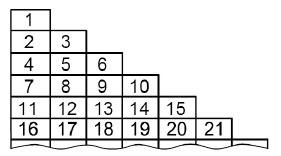
Варианты:
(А) 1 (Б) 4 (В) 5 (Г) 7 (Д) 13

23. Про натуральные числа m  и n  известно, что каждое из них делится на числа 2² * 3³ * 5 и 2³ * 3, а каждое из чисел 2⁵ * 3⁷ * 5³ и 2⁴ * 3⁶ * 5² делится на m  и n. Чему равно наибольшее возможное отношение чисел m  и n ?

 
Варианты:
(А) 2² * 3⁴ * 5²
(Б) 2 * З³
(В) 2² * 3³ * 5²
 (Г) 2 * 3² * 5
(Д) 2 * 3³ * 5

24.       Правильный треугольник «катится» вокруг квадрата (см. рисунок) Какую траекторию опишет отмеченная точка, прежде чем и она, и весь треугольник вернутся в исходное положение?

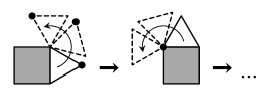
Варианты:

25.       Дробь 28/33  хотят представить в виде суммы нескольких дробей, числители
которых равны 1. При каком наименьшем числе слагаемых это возможно?
Варианты:
(А) 2   (Б) 3   (В) 4     (Г) 5    (Д) 28

26.       На плоскости нарисовано несколько прямых. Рядом с каждой прямой написано число прямых, которые ее пересекают. Среди написанных чисел имеется не менее четырёх различных, два из которых — это 6 и 7. Сколько прямых нарисовано?
Варианты:
(А) 9 (Б) 10 (В) 13 (Г) 15 (Д) невозможно определить
 

27.       В треугольнике длины сторон равны а, b и с, а угол, лежащий против стороны b, вдвое больше угла, лежащего против стороны а. Тогда обязательно
Варианты:
(А) а ² + с² = b²  
(Б) b² + bс = а²
(В) c² + ab = a²
(Г) а² + ас = b²
(Д) каждое из соотношений А-Г может быть нарушено

28. На рисунке ОА = 6 см, ОВ= 4 см. Каково множество всех точек Р, лежащих в первой четверти, для которых площадь четырёхугольника ОБ равна 24 см²?

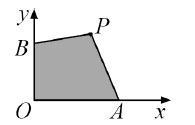
Варианты:

 
29. Назовём тройку различных чисел, выбранных из множества {1, 2, 3, 4, 5, 6}, хорошей, если никакая пара чисел из этой тройки не имеет сумму 7. Коля перемножил числа в каждой хорошей тройке, а потом сложил полученные произведения. Какое число он получил?
Варианты:
(А) 7²  (Б) 7³  (В) З⁶   (Г) 3⁷  (Д) 6³

 
30. Из 27 одинаковых маленьких кубиков сложили куб. Через середину его диагонали провели плоскость, перпендикулярную этой диагонали. Сколько маленьких кубиков пересекла эта плоскость?
Варианты:
(А) 17 (Б) 18  (В) 19  (Г) 20  (Д) 21

Ответы к конкурсу «Кенгуру»-2012 для 9-10 класса:

1. Г
2. А
3. Б
4. Г
5. Д
6. Б
7. Г
8. Д
9. А
10. Г
11. Б
12. В
13. Г
14. Г
15. В
16. Д
17. В
18. Б
19. В
20. В
21. Г
22. В
23. Д
24. А
25. Б
26. Б
27. Г
28. А
29. Б
30. В

Внимание

Простая снежинка из бумаги

Объемная (3D) снежинка из бумаги

Написать письмо Деду Морозу!!!

Крыса из бумаги на 2020 год!

Разносклоняемые существительные