Приближается международный математический конкурс «Кенгуру».
Предлагаем вам задания и ответы на «Кенгуру» для 5-6 классов 2011 года.
Ответы находятся внизу страницы, после заданий и перед комментариями.

Задачи, оцениваемые в 3 балла

1.         Вася пишет слово КЕНГУРУ по одной букве в день. Он начал в пятницу. В какой день недели он напишет последнюю букву?
Варианты:
(А) в понедельник (Б) во вторник (В) в среду (Г) в четверг (Д) в пятницу

2.         Гепард пробегает полкилометра за полминуты. С какой скоростью он бежит?
Варианты:
 (А) 90 км/час (Б) 75 км/час (В) 60 км/час (Г) 30 км/час  (Д) 15 км/час

3.         Квадратный лист бумаги разделили на две части одним прямым разрезом. Какая из фигур А— Г не могла при этом получиться?
Варианты:
 (А) шестиугольник (Б) пятиугольник (В) прямоугольник (Г) треугольник   (Д) все фигуры А — Г могут получиться

4.         Чему равна половина от третьей части удвоенного числа 3?
Варианты:
 (А)1/6 (Б)1/2 (В)1/3 (Г) 1 (Д)2

5.         В верхнюю трубу влили 120 литров воды. На каждой развилке поток воды делится на две равные части. Сколько литров воды попадет в резервуар У?

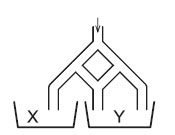
Варианты:
 (А) 100 (Б) 90 (В) 80 (Г) 60 (Д) 40

6.         Поль хотел умножить некоторое целое число на 301, но забыл про 0 и умножил на 31. В результате он получил число 372. А какой результат он должен был получить?
Варианты:
 (А) 3612 (Б) 3913 (В) 4214 (Г) 4515 (Д) 30720

7.         Если к сумме двух чисел прибавить их разность, то получится
Варианты:
 (A)     половина их суммы (Б) одно из двух данных чисел (B)            их удвоенная разность (Г) одно из этих чисел, деленное на 2 (Д) одно из этих чисел, умноженное на 2

8.         Дата 1 марта 2005 года может быть записана тремя последовательными нечетными числами, расположенными в порядке возрастания: 01.03.05. Сколько всего дат с таким свойством (включая названную) будет в нынешнем веке?
Варианты:
 (А) 5  (Б) 6    (В) 7    (Г) 15  (Д) 18

9. На пути в легендарную Страну Молока и Мёда хомячок Фридолин должен пройти через лабиринт, в котором лежат 16 тыквенных семечек. Какое наибольшее количество семечек хомячок сможет собрать, если нельзя проходить ни один коридор или перекресток больше одного раза?

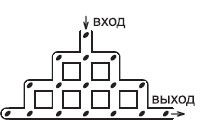
Варианты:
 (А) 10            (Б) 11 (В) 12  (Г) 13 (Д) 14

10.       В танцевальном классе всего 10 учеников. На 8 Марта мальчики принесли коробку с 80 конфетами и раздали девочкам по несколько конфет, всем поровну. После этого в коробке осталось еще 3 конфеты. Сколько мальчиков в этом классе?
Варианты:
 (А) 7  (Б) 6    (В) 5    (Г) 4    (Д)3

Задачи, оцениваемые в 4 балла

11.       Выпишем в порядке возрастания все четырехзначные числа, которые можно получить, переставляя цифры числа 2011. Чему равна разность между ближайшими соседями числа 2011 в этом ряду?
Варианты:
 (А) 890 (Б) 891 (В) 900 (Г) 909 (Д) 990

12.       Каким из блоков А — Д можно дополнить фигуру, изображенную ниже, до прямоугольного параллелепипеда?

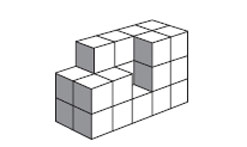
Варианты:

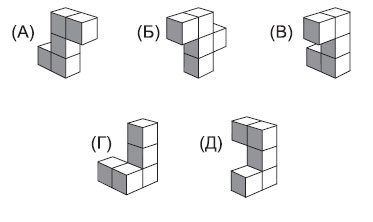
13.       Число а в полтора раза больше, чем число b. На сколько процентов a больше, чем b?
Варианты:
 (А) на 30 %   (Б) на 50%      (В) на 100% (Г) на 150%      (Д) ответ зависит от чисел а и b

14.       В трех играх футбольный клуб «Кенга» пропустил 1 мяч в свои ворота и забил 3 мяча в ворота противников. Одну игру клуб выиграл, одну игру проиграл и одну игру закончил вничью. Какой был счет в матче, который клуб «Кенга» выиграл?
Варианты:
 (А) 2 : 0 (Б) 3 : 0       (В) 1 : 0          (Г) 4: 1            (Д) 0: 1

15.       Вдоль шоссе расположены деревни А, В, С, D, Е, F и G (они перечислены в том порядке, в котором следуют друг за другом). В таблице указаны некоторые расстояния вдоль шоссе между этими деревнями (например, расстояние от В до Е по этой дороге равно 27 км). Чему равно расстояние от А до G?

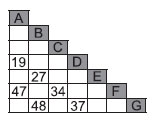
Варианты:
(А) 56 км (Б) 66 км (В) 75 км (Г) 18 км (Д) невозможно определить
 

16.       Каждый из четырех мальчиков либо всегда говорит правду, либо всегда лжет. Алекс говорит, что Ник — врун, Ник говорит, что Марк врун, Марк говорит, что Ник врун, Тони говорит, что Алекс врун. Сколько всего врунов среди них?
Варианты:
 (А) О (Б) 1    (В) 2    (0 3      (Д)4

17.       Наталья открыла полную банку компота. Когда она выловила и съела половину вишен из этой банки, уровень компота в ней стал ниже на одну треть. На сколько (по сравнению с этой новой высотой) понизится уровень компота, если Наталья съест половину оставшихся вишен?
Варианты:
 (А) на половину (Б) на треть         (В) на четверть (Г) на одну пятую (Д) невозможно определить

18.       Даниэль хочет составить квадрат из одинаковых фигурок, таких, как на рисунке. Каким наименьшим числом этих фигурок он может обойтись?

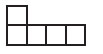
Варианты:
 (А) 8  (Б) 10  (В) 12  (Г) 16  (Д) 20

19.       У кошки семеро котят: белый, черный, рыжий, черно-белый, бело-рыжий, черно-рыжий и черно-бело-рыжий. Сколькими способами можно выбрать из этих котят четырех так, чтобы у любых двух выбранных котят был общий цвет?
Варианты: 
(А) 1 (Б)3 (В) 4 (Г)6 (Д)7

 
20. Какую цифру надо приписать к числу 25771, чтобы получившееся шестизначное число делилось на 12?
Варианты:
(А) 8   (Б) 6    (В) 4    (Г) 2    (Д)0

Задачи, оцениваемые в 5 баллов

21.       Возле любой вершины восьмиугольника надо написать одно из чисел 1, 2, 3 или 4. Три числа уже написаны (см. рисунок). Сколько раз будет написано число 4, если на концах каждого нарисованного отрезка, соединяющего две вершины, должны стоять разные числа?

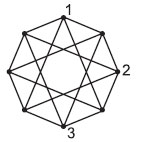
Варианты:
 (А) 1 (Б) 2 (В)3 (Г) 4 (Д) 5

22.       В некотором месяце было 5 суббот и 5 воскресений, но только 4 пятницы и 4 понедельника. Тогда в следующем месяце будет
Варианты:
 (А) 5 сред      (Б) 5 четвергов (В) 5 пятниц (Г) 5 суббот (Д) 5 воскресений

23.       Внутри прямоугольника 28x30 расположены 4 одинаковых прямоугольных треугольника. Точки Р и Q — середины сторон прямоугольника. Чему равна  площадь закрашенной фигуры?

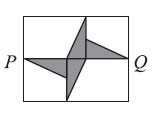
Варианты:
 (А) 46 (Б) 52 (В) 54 (Г) 56 (Д) 64

24.       Учитель задал на лето отличнику Пете и двоечнику Васе задачи, причем Васе — в 4 раза больше задач, чем Пете. После каникул оказалось, что Петя и Вася решили поровну задач, и процент задач, решенных Васей, равен проценту задач, не решенных Петей. Каков процент задач, решенных Петей?
Варианты:
 (А) 40%         (Б) 50%           (В) 60%          (Г) 80%           (Д) 90%

25.       Сколько существует трехзначных чисел, у которых сумма цифр меньше, чем 10, а произведение цифр — не больше, чем 10?
Варианты:
 (А) 6  (Б) 10  (В) 16  (Г) 80  (Д) 96

26.       Из трех стандартных игральных кубиков (общее число точек на любых двух противоположных гранях такого кубика равно 7) склеена «башня» так, что общее число точек на каждой паре склеенных граней равно 5. Потом все грани, кроме одной, закрасили. Сколько точек было на грани, отмеченной крестиком?

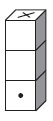
Варианты:
 (А) 2  (Б) 3    (В) 4    (Г) 5    (Д)6

27.       В числовом ребусе KxAxNxGxA=RxОхО буквами К, A, N, G, R, О обозначены разные цифры. Какое самое большое значение может принимать буква О?
Варианты:
 (А) 9  (Б) 8    (В) 7    (Г) 6    (Д) 5

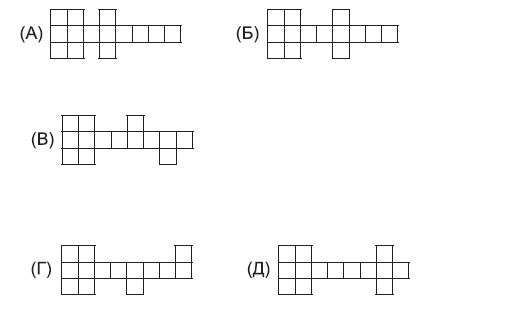
28.       Фигура, изображенная справа, склеена из бумаги. Какая из разверток А — Д не может получиться, если эту фигуру разрезать вдоль каких-то ребер и развернуть?

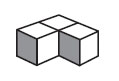
Варианты:

 
29.       Два пешехода идут навстречу друг другу: один из А в В, а другой — из В в А. Они вышли одновременно, и когда первый прошел половину пути, второму оставалось идти еще 1,5 часа, а когда второй прошел половину пути, то первому оставалось идти еще 45 минут. На сколько раньше закончит свой путь первый пешеход, чем второй?
Варианты:
 (А) 0,5 часа (Б) 1 час (В) 1,5 часа (Г) 2 часа (Д) 2,5 часа

30.       Все числа, сумма цифр которых делится на 5, выписывают в порядке возрастания. Чему равна самая маленькая разность между соседними числами в этом ряду?
Варианты:
 (А) 6  (Б) 5    (В) 4    (Г)3     (Д)1

Ответы:

1. (Г) в четверг
2. (В) 60 км/час
3. (А) шестиугольник
4. (Г) 1
5. (Б) 90
6. (А) 3612
7. (Д) одно из этих чисел, умноженное на 2
8. (А) 5
9. (Г) 13
10. (Д)3
11. (Б) 891
12.  (Д)
13. (Б) на 50%
14. (Б) 3 : 0
15. (А) 56 км
16. (В) 2
17. (В) на четверть
18. (Д) 20
19. (В) 4
20. (Г) 2
21. (Г) 4
22. (А) 5 сред
23. (Г) 56
24. (Г) 80%
25. (Д) 96
26. (Д)6
27.  (Б) 8
28.  (Г)
29. (А) 0,5 часа
30. (Д) 1

Внимание

Простая снежинка из бумаги

Объемная (3D) снежинка из бумаги

Написать письмо Деду Морозу!!!

Крыса из бумаги на 2020 год!

Разносклоняемые существительные