Кенгуру 2015 задания и ответы

Представляем задания и ответы на конкурс «Кенгуру-2015» для 9-10 классов.
Ответы на задания Кенгуру 2015 находятся после вопросов.

Задачи, оцениваемые в 3 балла
1. С первого января 2015 года малыш Федя начал вести дневник. Он уверен, что в каждом месяце 31 день, как и в январе. Какую дату он напишет в своем дневнике 19 марта 2015 года, в день конкурса «Кенгуру»?
Варианты ответов:
(A) 21 марта (Б) 16 марта (В) 22 марта (Г) 17 марта (Д) 18 марта

2. Петя катается на велосипеде по дорожкам парка, изображенным на рисунке. Он выехал из точки O в направлении, указанном стрелкой. На первом перекрестке Петя повернул направо, на втором — налево, потом опять направо, и так далее. В какой из точек А–Д он оказался раньше, чем в других?

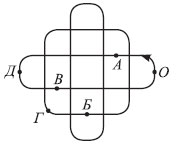
Варианты ответов:
(A) А (Б) Б (В) В (Г) Г (Д) Д

3. Что есть у параболы?
Варианты ответов:
(A) листва (Б) корневая система (В) верхушка (Г) ветви (Д) ствол

4. Во сколько раз секундная стрелка на часах вращается быстрее часовой?
Варианты ответов:
(A) 3600 (Б) 720 (В) 144 (Г) 120 (Д) 24

5. Капитан Сильвер помнит, что закопал клад не ближе, чем в 5 метрах от забора, и не дальше, чем в 5 метрах от пня старого дерева. На каком из рисунков заштрихована область, где может быть закопан клад?

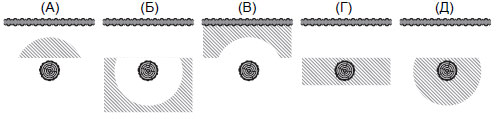
6. Сколько существует простых чисел, кубы которых меньше 1001?
Варианты ответов:
(A) 3 (Б) 4 (В) 5
(Г) 10 (Д) более 10

7. На рисунке изображена развертка прямой призмы. С каким ребром совпадет отрезок VU, если склеить эту призму?

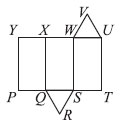
Варианты ответов:
(A) XY (Б) XW (В) VW (Г) ST (Д) RS

8. Известно, что x⁴= y⁴ и ( y - 1)²= 4. Чему не может равняться x?
Варианты ответов:
(A) -1 (Б) 1 (В) -3 (Г) 3 (Д) 2

9. Сторона квадрата на рисунке равна 1. Контур «бокала» образован одной полуокружностью и двумя четвертями окружностей с диаметрами 1 и с центрами на сторонах квадрата. Чему равна площадь «бокала»?

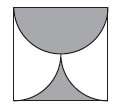
Варианты ответов:
(A)π/8
(Б)π/4
(В)π/2
(Г) 1/4
(Д) 1/2

10. Сколько сантидециметров в одном милликилометре?
Варианты ответов:
(A) 10⁶ (Б) 10⁵ (В) 10⁴ (Г) 10³ (Д) 10²

Задачи, оцениваемые в 4 балла

11. На сколько областей делят координатную плоскость три линии: ось Ox и две параболы y = 2 - x², y = x² - 1?
Варианты ответов:
(A) 7 (Б) 8 (В) 9 (Г) 10 (Д) 11

12. Незнайка говорит правду с полуночи до полудня и лжет с полудня до полуночи. Ежедневно он сочиняет стихи с 11:00 до 15:00. Сколько часов в сутках, когда он может гордо заявлять: «Сейчас я сочиняю стихи!»?
Варианты ответов:
(A) 1 (Б) 4 (В) 10 (Г) 12 (Д) 20

13. Сколько раз нужно последовательно применить операцию извлечения квадратного корня, чтобы, начав с числа 2015, впервые получить число, которое меньше 3?
Варианты ответов:
(A) 2 (Б) 3 (В) 4 (Г) 6 (Д) 7

14. Прямоугольник состоит из 12 одинаковых прямоугольников. Чему равно отношение AD : DC ?

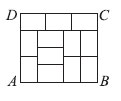
Варианты ответов:
(A) 4:5 (Б) 2:3 (В) 3:4 (Г) 7:9 (Д) 8:9

15. В прямоугольном треугольнике с катетами 4 и 5 провели медиану и высоту из вершины прямого угла. Чему равно произведение их длин?
Варианты ответов:
(A) 10 (Б) 2√41 (В) 5√41 (Г) 20 (Д) ½√41

16. Уравнение x² - 2 x + a = 0 имеет корни x₁ и x₂. Найдите x₁² - x₂² + 4 x₂.
Варианты ответов:
(A) 4 (Б) -4 (В) -2 (Г) 0 (Д) ответ зависит от a

17. На рисунке точка O — центр окружности, AB 􀀦CD, ED 􀀦 BC и угол EDC = 15°. Найдите угол EAD.

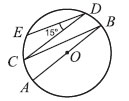
Варианты ответов:
(A) 15° (Б) 30° (В) 45°
(Г) 60° (Д) 75°

18. Длины ребер прямоугольного параллелепипеда — натуральные числа, а площади двух его граней равны 24 и 30. Какой наибольший объем может иметь этот параллелепипед?
Варианты ответов:
(A) 120 (Б) 240 (В) 360 (Г) 720 (Д) 1440

19. Назовем углы 40°, 50°, 90°, 100° красивыми. Сколько существует различных треугольников площади 1, все углы которых красивые?
Варианты ответов:
(A) 1 (Б) 2 (В) 3 (Г) 4 (Д) 5

20. За один шаг автомат может либо прибавить к данному натуральному числу, либо заменить это число на его наибольший простой делитель. За какое наименьшее число шагов из числа 2015 можно получить 2? (Заметьте, что 2015 = 31*13*5. )
Варианты ответов:
(A) 2 (Б) 3 (В) 4 (Г) 13 (Д) 34

Задачи, оцениваемые в 5 баллов

21. Придя в магазин, Винни-Пух обнаружил, что горшочек для меда подорожал на 60%, а мед подешевел на 60%, и теперь горшочек и мед в нем стоят поровну. Как изменилась цена горшочка с медом?
Варианты ответов:
(A) не изменилась (Б) уменьшилась на 30%
(В) увеличилась на 30% (Г) уменьшилась на 36%
(Д) уменьшилась на 20%

22. В семь областей на картинке нужно вписать семь чисел так, чтобы число в каждой области было равно сумме чисел во всех соседних областях (соседними считаются области, граничащие друг с другом по некоторой дуге). Два числа уже вписаны. Какое число придется вписать в центральную область?

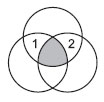
Варианты ответов:
(A) 0 (Б) - 3 (В) 3 (Г) - 6 (Д) 6

23. На доске написаны 10 различных чисел. Вася подчеркнул каждое число, которое равно произведению всех остальных девяти чисел. Какое наибольшее количество чисел может быть подчеркнуто?
Варианты ответов:
(A) 1 (Б) 2 (В) 3 (Г) 9 (Д) 10

24. Среди потомков Ивана Васильевича по мужской линии (сыновья, сыновья сыновей и т. д.) ровно 3 Ивана и 5 Васильевичей. При каком наименьшем числе потомков это возможно? (Имена любых двух братьев различны.)
Варианты ответов:
(A) 3 (Б) 5 (В) 6 (Г) 7 (Д) 8

25. На рисунке справа изображен график функции y = ƒ ( x).
На одном из рисунков А–Д изображен график фунции y = x ƒ ( x). На каком?

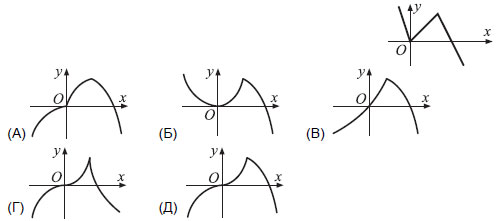
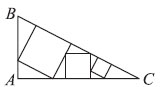
26. Внутри прямоугольного треугольника ABC расположено три квадрата, как на рисунке. Сторона самого маленького квадрата равна 1, а AB = 8.
Найдите сторону самого большого квадрата.

Варианты ответов:
(A) √2 (Б) 2 (В) 2√2 (Г) 3 (Д) 4

27. Вася выписал в тетрадь 30 различных целых чисел, каждое возвел либо в квадрат, либо в куб и записал полученные 30 результатов на доске. Какое наименьшее количество различных чисел могло оказаться на доске?
Варианты ответов:
(A) 1 (Б) 6 (В) 10 (Г) 15 (Д) 30

28. На прямой отмечено несколько точек. Выбрав одну из них, Федя подсчитал число отрезков с концами в других отмеченных точках, на которых она лежит. Получилось 80 отрезков. Проделав то же самое с другой отмеченной точкой, он получил 90 отрезков. Сколько точек было отмечено на прямой?
Варианты ответов:
(A) 20 (Б) 22 (В) 80 (Г) 90 (Д) невозможно определить

29. В турнире принимали участие спортсмены из двух стран. Каждый с каждым играл ровно один раз. В конце турнира оказалось, что число игр, где соперники были из разных стран, равно числу игр, где соперники были соотечественниками. Сколько могло быть участников?
Варианты ответов:
(A) 40 (Б) 57 (В) 63 (Г) 81 (Д) 99

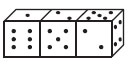
30. Три одинаковых игральных кубика приложены друг к другу одинаковыми гранями. При этом на верхних гранях «получилось» число 125 (см. рисунок). Сколько всего различных трехзначных чисел можно получить на верхних гранях, складывая кубики таким образом?

Варианты ответов:
(A) 96 (Б) 126 (В) 168 (Г) 192 (Д) 216

Ответы Кенгуру 2015 – 9-10 класс:
1. Б
2. В
3. Г
4. Б
5. Д
6. Б
7. А
8. Д
9. Д
10. Г
11. Г
12. В
13. Б
14. Д
15. А
16. А
17. В
18. Г
19. Б
20. Б
21. Г
22. А
23. Б
24. В
25. Д
26. Д
27. В
28. Б
29. Г
30. В