Представляем вниманию школьников задания и ответы на конкурс «Кенгуру-2014» для 7-8 классов.
Вопросы сгруппированы по сложности (по баллам).
Ответы на задания Кенгуру 2014 находятся после вопросов.
Задачи, оцениваемые в 3 балла
1. Каждый год конкурс «Кенгуру» проходит в третий четверг марта. Самый поздний из возможных дней для проведения конкурса — это
Варианты:
(A) 14 марта (Б) 15 марта (В) 20 марта (Г) 21 марта (Д) 22 марта
2. Марина разбирает бабушкины бусы. Она хочет снять ровно 5 темных бусин. Какое наибольшее количество белых бусин она сможет снять при этом?

Варианты:
(A) 4 (Б) 5 (В) 6 (Г) 7 (Д) 8
3. Какое слово написано правильно?
Варианты:
(A) параллеллограмм (Б) пароллелограмм (В) параллелограм
(Г) паралелограмм (Д) параллелограмм
4. В остроугольном треугольнике ABC проведены высота BH и биссектриса AD, пересекающиеся в точке O. Оказалось, что угол AOB в четыре раза больше угла DAB. Чему равен угол CAB ?
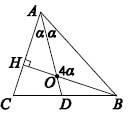
Варианты:
5. Если при увеличении всех сторон квадрата на 1 его площадь увеличилась на 37, то сторона исходного квадрата равна
Варианты:
(A) 6 (Б) 16 (В) 18 (Г) 19 (Д) 36
6. Если b = a + 7, c = b - 9, d = c + 4, то какое из чисел a, b, c и d наибольшее?
Варианты:
(A) a (Б) b (В) c (Г) d (Д) невозможно определить
7. Какое из произведений наибольшее?
Варианты:
(A) 44 х 777 (Б) 55 х 666 (В) 77 х 444 (Г) 88 х 333 (Д) 99 х 222
8. Отношение произведения двух чисел к частному этих чисел всегда равно
Варианты:
(A) квадрату одного из чисел (Б) сумме этих чисел
(В) одному из этих чисел (Г) обратному к одному из чисел
(Д) ничему из перечисленного
9. Куб 3 x 3 x 3 сложен из 13 белых и 14 темных кубиков. На каком из рисунков А – Д он изображен?
Варианты:

10. Вася ходит на кружок по математике два раза в неделю, а Петя — на кружок по биологии раз в две недели. Оказалось, что за несколько недель у Васи занятий кружка было на 15 больше, чем у Пети. Сколько недель длился этот период?
Варианты:
(A) 30 (Б) 25 (В) 20 (Г) 15 (Д) 10
Задачи, оцениваемые в 4 балла
11. Капитан Флинт и несколько пиратов нашли сундук с золотыми монетами. Они разделили монеты поровну. Если бы пиратов было на 4 меньше, то каждый получил бы на 10 монет больше. Если бы монет было на 50 меньше, то каждый пират получил бы на пять монет меньше. Сколько золотых монет было в сундуке?
Варианты:
(A) 80 (Б) 100 (В) 120 (Г) 150 (Д) 250
12. Братья Эд и Бен ездят в школу на самокатах. Бен выезжает из дома в 8 : 00 и приезжает в 8 : 40. Эд выезжает на пять минут раньше и приезжает в школу на 15 минут позже Бена. В какое время Бен перегоняет Эда?
Варианты:
(A) 8 : 05 (Б) 8 : 10 (В) 8 : 15 (Г) 8 : 20 (Д) 8 : 25
13. В клетки квадрата 3 x 3 вписаны числа 1, 2, …, 9. Назовем числа соседними, если они написаны в клетках, имеющих общую сторону. Известно, что в угловые клетки вписаны числа 1, 2, 3 и 4 (см. рисунок), и сумма чисел, соседних с числом 9, равна 15. Чему равна сумма чисел, соседних с числом 8?
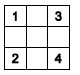
Варианты:
(A) 12 (Б) 15 (В) 16 (Г) 26 (Д) 27
14. Квадрат числа n равен 2014 . Сколько цифр в десятичной записи числа n?
Варианты:
(A) 4 (Б) 9 (В) 10 (Г) 11 (Д) 14
15. На листе клетчатой бумаги отмечено 15 точек (см. рисунок). Таня провела несколько параллельных прямых так, что каждая отмеченная точка лежит на одной из проведенных прямых, и на каждой из этих прямых есть хотя бы одна отмеченная точка. Сколько прямых не могло получиться у Тани?

Варианты:
(A) 3 (Б) 4 (В) 5 (Г) 7 (Д) 9
16. Про числа x и y известно, что x не равно y и ( x -1)2 +3x = ( y -1)2 +3 y . Чему равна сумма этих чисел?
Варианты:
(A) -1 (Б) 0 (В) 1 (Г) 2 (Д) невозможно определить
17. Чему не может быть равна разность двух простых чисел?
Варианты:
(A) 5 (Б) 6 (В) 7 (Г) 8 (Д) 9
18. Пять одинаковых маленьких прямоугольников расположены внутри прямоугольника 33 х 32 так, как показано на рисунке. Чему равна площадь одного маленького прямоугольника?
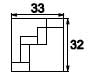
Варианты:
(A) 50 (Б) 55 (В) 60 (Г) 72
(Д) невозможно определить
19. Если среднее арифметическое двух положительных чисел на 30 % меньшебольшего из этих чисел, то оно больше меньшего из них на
Варианты:
(A) 75 % (Б) 70 % (В) 30 % (Г) 25 % (Д) 20 %
20. Из нескольких одинаковых кубиков Вася сложил большой куб и покрасил его грани. Оказалось, что число кубиков с одной покрашенной гранью равно числу кубиков, у которых покрашенных граней нет. Сколько маленьких кубиков использовал Вася?
Варианты:
(A) 27 (Б) 64 (В) 125 (Г) 216 (Д) 512
Задачи, оцениваемые в 5 баллов
21. Старые весы работают так: если вес груза на них не больше 1000 г, то весы показывают правильный вес, а в противном случае они показывают произвольный вес, больший 1000 г. Есть пять гирь с весами A, B, C, D и E. При взвешивании нескольких пар гирь эти весы показали, что B + D = 1200 г, C + E = 2100 г, B + E = 800 г, B + C = 900 г, A + E = 700 г. Какая гиря самая тяжелая?
Варианты:
(A) A (Б) B (В) C (Г) D (Д) E
22. Вася и Петя соревнуются в решении задач. Им предложено 100 задач, причем за каждую решенную задачу тот, кто решил ее первым, получает 4 балла, а тот, кто решил ее вторым, получает 1 балл. Вася и Петя решили по 60 задач и вместе набрали 312 баллов. Сколько задач решены обоими мальчиками?
Варианты:
(A) 57 (Б) 56 (В) 55 (Г) 54 (Д) 53
23. Дима выписал все числа от 1 до 2014. На сколько больше он написал единиц, чем троек?
Варианты:
(A) 5 (Б) 251 (В) 1004 (Г) 1005 (Д) 2014
24. На рисунке 1 изображен один и тот же кубик в разных положениях. Из четырех таких кубиков сложена фигура, передняя грань которой изображена на рисунке 2. Как выглядит противоположная грань этой фигуры?
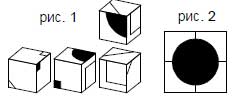
Варианты:

25. Федя поехал на велосипеде из города в деревню. Он собирался приехать в деревню ровно в 15 : 00. За две трети отведенного времени он проехал три четверти пути. После этого он изменил скорость и прибыл в деревню в 15 : 00, как и собирался. Чему равно отношение его первоначальной скоро- сти к скорости на последней четверти пути?
Варианты:
(A) 5 : 4 (Б) 4 : 3 (В) 3 : 2 (Г) 2 : 1 (Д) 3 : 1
26. При умножении натурального числа на 2 сумма цифр не может
Варианты:
(A) остаться прежней (Б) уменьшиться в два раза (В) уменьшиться в 4 раза
(Г) уменьшиться в 5 раз (Д) все события A – Г возможны
27. На острове живут рыцари, которые всегда говорят правду, лжецы, которые всегда лгут, и хитрецы, каждый из которых поочередно отвечает на заданные ему вопросы то правду, то ложь. Каждому жителю острова было задано два вопроса: «Вы рыцарь?» и затем «Вы хитрец?». Ответ «Да» на первый вопрос дали 17 человек, а на второй — 12. Сколько рыцарей на острове?
Варианты:
(A) 4 (Б) 5 (В) 17 (Г) 29 (Д) невозможно определить
28. В параллелограмме ABCD биссектриса угла A проходит через середину стороны BC, а угол BDC
равен 90 градусов. Чему равен угол BAD?
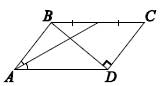
Варианты:
29. Пусть N — наименьшее число, все остатки от деления которого на 2, 4, 6, …, 100 различны. Какой остаток дает N при делении на 100?
Варианты:
(A) 0 (Б) 1 (В) 50 (Г) 98 (Д) 99
30. Квадрат разрезали на прямоугольники так, что любая прямая, параллельная одной из сторон квадрата и не содержащая сторон прямоугольников, пересекает ровно 40 прямоугольников. На какое наименьшее число прямоугольников мог быть разрезан квадрат?
Варианты:
(A) 80 (Б) 156 (В) 160 (Г) 1600 (Д) 3200
Ответы Кенгуру 2014 - 7-8 класс:

Внимание
Объемная (3D) снежинка из бумаги
Написать письмо Деду Морозу!!!
Разносклоняемые существительные


