Представляем вниманию школьников задания и ответы на конкурс «Кенгуру-2014» для 9-10 классов.
Вопросы сгруппированы по сложности (по баллам).
Ответы на задания Кенгуру 2014 находятся после вопросов.
Задачи, оцениваемые в 3 балла
1. Кенгуру изготовил личную печать (см. рисунок). Какой из отпечатков А–Д можно сделать такой печатью?


2. Во сколько раз отношение чисел 7 и 8 меньше произведения этих же чисел?
(A) 14 (Б) 16 (В) 42 (Г) 56 (Д) 64
3. Маша нарисовала квадрат и правильный треугольник. Оказалось, что площадь квадрата равна квадрату периметра треугольника. Во сколько раз сторона квадрата больше стороны треугольника?
(A) 2 (Б) 3 (В) 4 (Г) 6 (Д) они равны
4.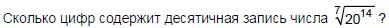
(A) 2 (Б) 3 (В) 4 (Г) 7 (Д) 10
5. Какое из слов написано правильно?
(A) параллелопипед (Б) паралелепипед (В) паралелопипед
(Г) паралеллепипед (Д) параллелепипед
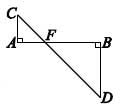
6. Длина отрезка АВ равна 20. Треугольники CAF и FBD — прямоугольные и равнобедренные. Чему равна длина замкнутой ломаной ACDBA?
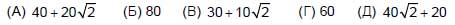
7. В Цветочном городе месяц считается хорошим, если в нём солнечных дней ровно в два раза больше, чем пасмурных. Какое наибольшее количество хороших месяцев может быть в году?
(A) 3 (Б) 4 (В) 5 (Г) 6 (Д) 12
8. Чему не может равняться разность двух простых чисел?
(A) 10 (Б) 11 (В) 12 (Г) 13 (Д) 14
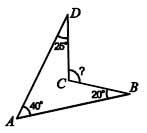
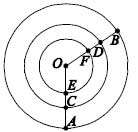
9. Найдите угол BCD.
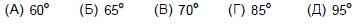
10. Дима придумал операцию возведения в «суперстепень»:
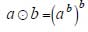

Задачи, оцениваемые в 4 балла
11. На глобусе нарисовали 10 параллелей (окружностей) и 10 меридианов (полуокружностей). На сколько частей они делят поверхность глобуса?
(A) 20 (Б) 21 (В) 100 (Г) 110 (Д) 121
12. Вася заметил, что числа 1, -2, -3 — все корни уравнения x3+ 4 x2+ x -6 =0. После этого он легко нашёл все действительные корни уравнения x6+ 4 x4+ x2- 6 = 0. Сколько их оказалось?
(A) 1 (Б) 2 (В) 3 (Г) 4 (Д) 6
13. На рисунке изображены три концентрические окружности с центром О. Угол АОВ равен 120o . Какой из следующих путей самый короткий?

14. На доске выписаны числа 1, 2, 3, …, 99, 100. Том хочет стереть некоторые из этих чисел так, чтобы произведение оставшихся не делилось на 18. Какое наименьшее количество чисел ему придётся стереть?
(A) 50 (Б) 33 (В) 32 (Г) 31 (Д) 11
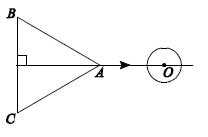
15. Правильный треугольник АВС, высота которого равна 5 см, движется по плоскости со скоростью 1 см / мин в направлении, указанном стрелкой. Сколько минут круг радиуса 1 см с центром О будет полностью закрыт треугольником?
(A) 1 (Б) 2 (В) 2,5
(Г) 3 (Д) 5
16. Если среднее арифметическое двух положительных чисел на 75 % больше меньшего из этих чисел, то оно меньше большего из них на
(A) 30 % (Б) 40 % (В) 70 % (Г) 75 % (Д) 80 %
17. Через 5 часов до полуночи останется вдвое меньше времени, чем 9 часов назад оставалось до полудня. Через сколько часов наступит полночь?
(A) 4 (Б) 5 (В) 6 (Г) 7 (Д) 8
18. График функции y = f ( x ) симметричен относительно прямой x = 4 и уравнение f ( x ) = 0 имеет 7 различных действительных корней. Чему равна сумма этих корней?
(A) 18 (Б) 20 (В) 24 (Г) 28 (Д) 32
19. Малыш, Карлсон и Винни-Пух ели варенье. Они начали одновременно и ели до тех пор, пока варенье не кончилось. Малыш успел съесть только одну девятую часть варенья. Если бы ели только Малыш и Карлсон, то Малышу досталась бы четверть всего варенья. Какая часть варенья досталась бы Малышу, если бы он ел только с Винни-Пухом?
20. На гранях кубика Даша нарисовала отрезки, образующие шестиугольник.
На каком из рисунков А–Д изображена развертка этого кубика?

Задачи, оцениваемые в 5 баллов
21. Найдите первую цифру наименьшего из чисел, которые делятся на 4 и имеют сумму цифр 1000.
(A) 2 (Б) 3 (В) 4 (Г) 6 (Д) 9
22. На олимпиаде было предложено 10 задач. Председатель жюри сообщил, что не каждый участник не решил не более трёх задач. Что это означает?
(A) Каждый участник решил не более трёх задач.
(Б) Каждый участник решил менее семи задач.
(В) Кто-то из участников решил не более трёх задач.
(Г) Кто-то из участников решил менее семи задач.
(Д) Никто из участников не решил более семи задач.
23. Маша нарисовала на координатной плоскости 5 парабол вида y=x2+bx +c и отметила все их точки пересечения. Каким не могло получиться количество отмеченных точек?
(A) 1 (Б) 3 (В) 4 (Г) 5 (Д) 6
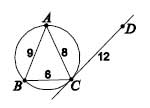
24. Точки А, В, С лежат на окружности и АВ = 9, АС = 8, ВС = 6. Прямая DC касается окружности, и DC = 12. Найдите длину отрезка AD.
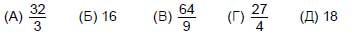
25. Какое наибольшее значение можно получить, расставляя скобки в выражении 1 - 2 + 3 - 4 + 5 - 6 + 7 - 8 + 9 - 10?
(A) 15 (Б) 39 (В) 45 (Г) 50 (Д) 55
26. Число N равно произведению 2014 простых чисел (не обязательно различных). Каждое из этих простых чисел увеличили на 1 и перемножили 2014 новых чисел, получив число М. Для скольких натуральных чисел N число М делится на N ?
(A) 0 (Б) 112 (В) 336 (Г) 2014
(Д) таких N бесконечно много
27. В треугольнике АВС биссектриса СD равна стороне АС. Какое из утверждений А–Г может быть неверным?
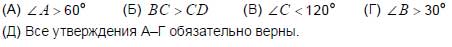
28. Все натуральные числа, полученные из числа 1234567 перестановкой цифр, включая это число, выписали в возрастающем порядке. Каким числом заканчивается первая половина этого списка?
(A) 3765421 (Б) 4123567 (В) 4352617 (Г) 4376512 (Д) 4376521
29. Через точку внутри треугольной пирамиды провели четыре различные плоскости, каждая из которых параллельна одной из граней пирамиды. На сколько частей эти плоскости разбивают пирамиду?
(A) 10 (Б) 12 (В) 14 (Г) 15 (Д) 16
30. Васины часы идут абсолютно точно, но минутная и часовая стрелки на них выглядят одинаково. Сколько раз между полуночью и полуднем по этим часам нельзя определить время?
(A) 120 (Б) 132 (В) 134 (Г) 142 (Д) 144
Ответы Кенгуру 2014 - 9-10 класс:
Внимание
Объемная (3D) снежинка из бумаги
Написать письмо Деду Морозу!!!
Разносклоняемые существительные


