Представляем вниманию школьников задания и ответы на конкурс «Кенгуру-2013» для 9-10 классов.
Вопросы сгруппированы по сложности (по баллам).
Ответы на задания находятся после вопросов.
Задачи, оцениваемые в 3 балла
1. В каком слове можно найти каждую из букв слова КЕНГУРУ?
(A) ПРЯМОУГОЛЬНИК (Б) ПАРАБОЛА (В) ТРЕУГОЛЬНИК (Г) ГИПОТЕНУЗА (Д) ГИПЕРБОЛА
2. 415 + 810 равно
(A) 210 (Б) 215 (В) 220 (Г) 230 (Д) 231
3. На клетчатом листке отметили 6 точек (сторона клеточки равна 1). У каждого треугольника с вершинами в отмеченных точках нашли площадь. Самая маленькая из этих
площадей равна
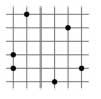
(A) 1/4
(Б) 1/2
(В) 1
(Г) 3/2
(Д) 2
4. Маша придумала новую алгебраическую операцию: a x b = a + 2b . Найдите
(a x a ) *(b x a ) .
(A) 7a + 2b (Б) 5a + 2b (В) 3a + 2b (Г) 5a + b (Д) 7a + b
5. Какое из чисел А–Д самое большое?
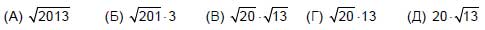
6. На рисунке угол Альфа = 55 градусов, Бетта = 40 градусов, Гамма = 35 градусов. Найдите угол Сигма .
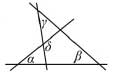
(A) 120 градусов (Б) 125 градусов (В) 130 градусов (Г) 135 градусов (Д) 140 градусов
7. Вчера Васин дедушка, отмечая свой день рождения, сказал: «Вот мне и пошел восьмой десяток!» Вася, который любит все считать в дюжинах, сообщил, что восьмая дюжина пойдет дедушке через
(A) 2 года (Б) 4 года (В) 12 лет (Г) 14 лет (Д) 16 лет
8. Какая получится картинка, если дугу со стрелкой на рисунке справа сначала повернуть вокруг точки O на 90 градусов против часовой стрелки, а потом отразить симметрично относительно оси OX ?
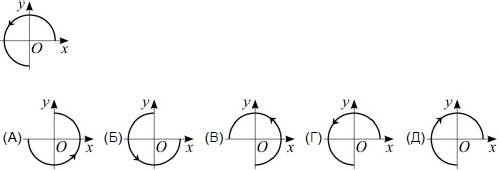
9. Число n — самое большое из натуральных чисел, для которых 4n трехзначно. Число m — самое маленькое из натуральных чисел, для которых 4m трехзначно. Чему равна разность 4n - 4m?
(A) 900 (Б) 899 (В) 896 (Г) 225 (Д) 224
10. Прямоугольник ABCD лежит в I четверти. Его стороны параллельны осям координат (см. рисунок). Для какой из его вершин отношение ординаты к абсциссе является наибольшим?
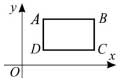
(A) A (Б) B (В) C (Г) D
(Д) ответ зависит от размеров прямоугольника
Задачи, оцениваемые в 4 балла
11. Ученики 11А класса написали тест. Если бы каждый мальчик получил на 3 балла больше, то средний результат класса был бы на 1,2 балла выше. Сколько процентов составляют в этом классе девочки?
(A) 20 % (Б) 30 % (В) 40 % (Г) 50 % (Д) 60 %
12. Если длины сторон трапеции — целые числа, то ее периметр не может быть равен
(A) 5 (Б) 6 (В) 7 (Г) 8 (Д) 2013
13. Из чисел 1, 2, 3, …, 30 выбрали набор, в котором ровно четыре числа делятся на 4, ровно три делятся на 6 и ровно четыре делятся на 5. Какое наименьшее количество чисел могло быть в таком наборе?
(A) 6 (Б) 7 (В) 8 (Г) 9 (Д) 11
14. Сколько корней имеет уравнение
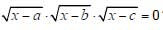
?
(A) 0 (Б) 1 (В) 2 (Г) 3 (Д) ответ зависит от a, b, c
15. На рисунке справа изображены две окружности с общим центром. Хорда AB большей окружности имеет длину 20 и касается меньшей окружности. Чему равна площадь
заштрихованного кольца?

16. Назовем началом отрезка на числовой оси его первую половину, а его концом — вторую половину. Какой отрезок является началом того конца, которым оканчивается начало отрезка [0; 8]?
(A) [1; 2] (Б) [2; 3] (В) [3; 4] (Г) [5; 6] (Д) [6; 7]
17. У какой прямой на координатной плоскости удвоенная сумма ординаты и утроенной абсциссы для каждой точки равна 6?
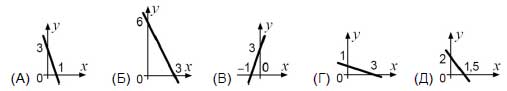
18. Назовем треугольник ABC нормальным, если из его высот можно составить новый треугольник. Сколько из треугольников на рисунке нормальные?

(A) 1 (Б) 2 (В) 3 (Г) 4 (Д) 5
19. Все члены каждого из клубов «Толстяки» и «Пухляки» имеют разный вес. Малыш Федя состоит в обоих клубах. Известно, что он самый тяжелый толстяк среди пухляков и самый легкий пухляк среди толстяков. Тогда обязательно
(A) Федя — самый тяжелый толстяк.
(Б) Федя — самый легкий пухляк.
(В) Любой пухляк весит не меньше, чем любой толстяк.
(Г) Федя — единственный, кто состоит в обоих клубах.
(Д) любое из утверждений А–Г может быть неверным.
20. Чему равна сумма x + y, если x2- 6x = 2xy - x2- y2- 9?
(A) 0 (Б) 3 (В) 6 (Г) 9 (Д) невозможно определить
Задачи, оцениваемые в 5 баллов
21. Биссектриса BL угла B в треугольнике ABC делит сторону AC в отношении 1 : 2 ( AL : LC = 1: 2 ). Какой угол образует эта биссектриса с медианой, проведенной из вершины A?
(A) 20 градусов (Б) 30 градусов (В) 45 градусов (Г) 60 градусов (Д) 90 градусов
22. Если 3 f ( x)+ f (-x) = x2+ 2x для всех x , то число f (2 ) равно
(A) 2 (Б) 3 (В) 4 (Г) 5 (Д) 6
23. Вася разбивает на пары натуральные числа от 1 до 22 и подсчитывает количество пар, в которых одно из чисел делится на другое. Какой наибольший результат у него может получиться?
(A) 7 (Б) 8 (В) 9 (Г) 10 (Д) 11
24. Из точки A выезжает автомобиль и едет по прямой дороге со скоростью 50 км/ч. Затем каждый час из A выезжает новый автомобиль, причем каждый следующий едет на 1 км/ч быстрее предыдущего. Последний автомобиль выезжает через 50 часов после первого и едет со скоростью 100 км/ч. Какова скорость автомобиля, который будет возглавлять колонну через 100 часов после старта первого автомобиля?
(A) 50 км/ч (Б) 66 км/ч (В) 75 км/ч (Г) 84 км/ч (Д) 100 км/ч
25. Прямые, содержащие стороны треугольника ABC, образуют с некоторой прямой углы 30 градусов, 40 градусов и 80 градусов.
Какое наибольшее значение может принимать угол этого треугольника?
(A) 70 градусов (Б) 90 градусов (В) 110 градусов (Г) 130 градусов (Д) 150 градусов
26. Назовем натуральное число n богатым, если сумма всех его натуральных делителей больше 2n. Например, число 12 является богатым, так как 1+ 2 + 3 + 4 + 6 +12 > 24 . Каким не может быть богатое число?
(A) точным квадратом (Б) числом, кратным 2013 (В) больше миллиона
(Г) степенью числа 3 (Д) каждое из свойств А–Г возможно
27. Числа 1, 2, 3, …, 10 выписаны по кругу в произвольном порядке. Складывая каждое из этих чисел с двумя его «соседями», мы получим 10 сумм. Пусть A — это наименьшая из этих сумм. Найдите наибольшее возможное значение A.
(A) 13 (Б) 14 (В) 15 (Г) 16 (Д) 17
28. Фигурками какого из видов А–Г нельзя «замостить» плоскость (без наложений)?

29. Вдоль дороги растут дубы и березы, всего 100 деревьев. Количество деревьев между любыми двумя дубами не равно 5. Какое наибольшее количество дубов может быть среди этих 100 деревьев?
(A) 17 (Б) 50 (В) 51 (Г) 52 (Д) 53
30. Вася проводит на плоскости прямые так, что никакие две из них не параллельны и никакие три не проходят через одну точку. Он хочет, чтобы все треугольники, образованные этими прямыми, были тупоугольными. Какое наибольшее число прямых он сможет провести?
(A) 4 (Б) 5 (В) 6 (Г) 7 (Д) сколько угодно
Ответы на конкурс «Кенгуру»-2013 для 9-10 класса:
1-в
2-д
3-б
4-а
5-д
6-в
7-г
8-Д
9-в
10-а
11-Д
12-Б
13-Б
14-Б
15-Д
16-Б
17-А
18-В
19-Г
20-В
21-Д
22-Б
23-Г
24-В
25-Г
26-Г
27-В
28-Д
29-Г
30-Д
Внимание
Объемная (3D) снежинка из бумаги
Написать письмо Деду Морозу!!!
Разносклоняемые существительные


