Представляем вниманию школьников задания и ответы на конкурс «Кенгуру-2013» для 5-6 классов.
Вопросы сгруппированы по сложности (по баллам).
Ответы на задания находятся после вопросов.
Задачи, оцениваемые в 3 балла
1. Вася написал слово КЕНГУРУ. Сколько из этих букв он мог написать, не отрывая карандаша от бумаги и не проходя по одной линии дважды?
Варианты:
(A) 1 (Б) 2 (В) 3 (Г) 4 (Д) 5
2. Сколько маленьких кубиков надо добавить к фигуре, изображенной справа, чтобы получить фигуру, изображенную слева?
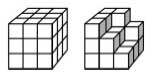
Варианты:
(A) 5 (Б) 6 (В) 7 (Г) 8 (Д) 9
3. В декабре черепашка Паша проспала ровно три недели. Сколько минут в декабре она бодрствовала?
Варианты:
(A) (31- 7) х 3 х 24 х 60
(Б) (31- 7 х 3) х 24 х 60 х 60
(В) (30 - 7 х 3) х 24 х 60
(Г) (31- 7) х 24 х 60
(Д) (31- 7 х 3) х 24 х 60
4. Коля учится водить автомобиль. Он уже умеет поворачивать направо, но еще не умеет поворачивать налево. Ему надо проехать из точки А в точку В.
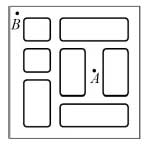
Наименьшее количество поворотов, которое ему придется сделать, равно
Варианты:
(A) 4 (Б) 5 (В) 6 (Г) 8 (Д) 10
5. Сколько минут проходит от середины второй четверти часа до середины его четвертой четверти?
Варианты:
(A) 15 (Б) 20 (В) 30 (Г) 40 (Д) 45
6. Какой результат не может получиться, если перемножить три однозначных числа?
Варианты:
(A) 288 (Б) 125 (В) 72 (Г) 63 (Д) 39
7. Если 1111 : 101 = A, то чему равно 3333 : 101 + 6666 : 303?
Варианты:
(A) 2 A (Б) 3 A (В) 5 A (Г) 6 A (Д) 9 A
8. Две пересекающиеся окружности разбивают плоскость на четыре части (см. рисунок). На какое наибольшее число частей могут разбить плоскость два квадрата?
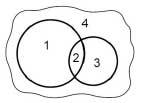
Варианты:
(A) 4 (Б) 7 (В) 9 (Г) 10 (Д) 12
9. В воскресение утром длина червячка Кеши была 6 см. К вечеру его длина увеличилась на половину от утренней, а за ночь его длина увеличилась на треть от вечерней. Какой стала длина червячка Кеши в понедельник утром?
Варианты:
(A) 10 см (Б) 11 см (В) 12 см (Г) 13 см (Д) 14 см
10. Каждые 10 минут Аня зажигает по свечке. Каждая свечка горит в течение 40 минут, а затем гаснет. Сколько свечей будет гореть через 65 минут после того, как Аня зажжет первую свечку?
Варианты:
(A) 3 (Б) 4 (В) 5 (Г) 6 (Д) 7
Задачи, оцениваемые в 4 балла
11. Вчера Васин дедушка отмечал день рождения. Он сказал: «Вот мне и пошел седьмой десяток!» Вася, который любит все считать дюжинами, добавил: «Дедушка, тебе пошла … дюжина». Какое слово пропущено?
Варианты:
(A) третья (Б) четвертая (В) пятая (Г) шестая (Д) седьмая
12. Маша нарисовала на квадратных листках бумаги несколько фигурок (их стороны параллельны краям листа).

Сколько из них имеют такой же периметр, как и сам лист бумаги?
Варианты:
(A) 1 (Б) 2 (В) 3 (Г) 4 (Д) 5
13. Коля выписал числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 и подчеркнул 3 нечётных числа. После этого он подчеркнул 2 других числа, каждое из которых делится на 3. Наконец, он сложил все 5 подчёркнутых чисел. Какую самую маленькую сумму он мог получить?
Варианты:
(A) 18 (Б) 20 (В) 22 (Г) 24 (Д) 25
14. На каждой клеточке квадрата 4?4 (см. рисунок) построена «башенка» из одинаковых кубиков. Число кубиков в каждой башенке равно числу, написанному в соответствующей
клеточке. Что мы увидим, если посмотрим на эту конструкцию со стороны, указанной стрелочкой?

15. Сколько существует пар двузначных чисел, разность которых равна 50?
Варианты:
(A) 30 (Б) 39 (В) 40 (Г) 49 (Д) 50
16. Чудо-автомат изменяет любую тройку чисел по такому правилу: каждое число он меняет на сумму двух остальных. Например, из тройки {3, 4, 6} на первом шаге получается {10, 9, 7}, на втором шаге — {16, 17, 19}, и так далее. Какой будет разность между самым большим и самым маленьким числами в тройке, полученной из {20, 1, 3} за 2013 шагов?
Варианты:
(A) 19 (Б) 41 (В) 117 (Г) 543 (Д) 2013
17. В первом тайме футбольного матча между командами Шайба и Зубило было забито 6 голов, и к концу тайма команда Зубило вела в счете. Во втором тайме команда Шайба забила 3 гола и выиграла матч. Сколько всего голов забила команда Шайба?
Варианты:
(A) 3 (Б) 4 (В) 5 (Г) 6 (Д) 7
18. Если из куба 3х3х3 вырезать угловой кубик 1х1х1, то получится фигура, имеющая 9 граней (см. рисунок). Сколько граней будет иметь фигура, которая получится, если
вырезать все остальные угловые кубики?
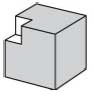
Варианты:
(A)16 (Б) 20 (В) 24 (Г) 30 (Д) 36
19. Коты Тоша и Малыш разлеглись на диване. Тоша лег первый, а потом лег Малыш, который занял четверть свободного места. Вместе они заняли ровно половину дивана. Какую часть дивана занял Тоша?
Варианты:
(A) 1/2
(Б) 1/3
(В) 1/4
(Г) 1/6
(Д) 1/12
20. Фермер собирается отвезти на рынок яйца: 135 коричневых и 162 белых. Он хочет упаковать их в одинаковые контейнеры так, чтобы в каждом контейнере все яйца имели один и тот же цвет, и свободных мест в контейнерах не было. Каким наименьшим числом контейнеров может обойтись фермер?
Варианты:
(A) 11 (Б) 27 (В) 33 (Г) 54 (Д) 297
Задачи, оцениваемые в 5 баллов
21. В ряд расположены 4 кнопки (см. рисунок). На двух изображены грустные лица, а на двух — веселые. Если нажать на любую кнопку, то на ней и на соседних кнопках выражение лица поменяется на противоположное. За какое наименьшее число нажатий можно сделать веселыми лица на всех кнопках?

Варианты:
(A) 2 (Б) 3 (В) 4 (Г) 5 (Д) 6
22. Сколько трехзначных чисел обладает следующим свойством: если из такого числа вычесть 297, то получится трехзначное число, записанное теми же цифрами, но в обратном порядке?
Варианты:
(A) 6 (Б) 7 (В) 10 (Г) 60 (Д) 70
23. Вася разбивает на пары натуральные числа от 1 до 22 и подсчитывает количество пар, в которых одно из чисел делится на другое. Какой наибольший результат у него может получиться?
Варианты:
(A) 7 (Б) 8 (В) 9 (Г) 10 (Д) 11
24. Какими фигурками нельзя «замостить» плоскость без наложений?
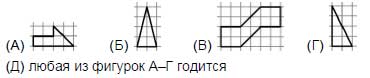
25. 40 мальчиков и 28 девочек встали в круг. Ровно у 18 мальчиков соседка справа — девочка. У скольких мальчиков соседка слева — девочка?
Варианты:
(A)10 (Б) 18 (В) 22 (Г) 28 (Д) невозможно определить
26. На стене висят двое часов. Одни часы показывают точное время, а другие спешат. Сейчас угол между часовыми стрелками этих часов равен 72 градусов. Чему равен угол между минутными стрелками этих часов?
Варианты:
(A) 144 градуса (Б) 120 градусов (В) 84 градусам (Г) 21 градусу (Д) 7 градусам
27. Буратино расставляет по кругу целые числа от 1 до 100, а папа Карло дает Буратино по 1 золотому за каждое число, которое больше суммы двух своих соседей. Какое наибольшее количество золотых может получить Буратино?
Варианты:
(A) 51 (Б) 50 (В) 49 (Г) 34 (Д) 25
28. На острове было 2013 жителей. Некоторые из них рыцари, а остальные — лжецы. Рыцари говорят только правду, а лжецы всегда лгут. Каждый день один из жителей произносил: «Когда я уеду, на острове станет поровну рыцарей и лжецов». Сказав это, он покидал остров. Никто из них не возвращался, и после 2013 дней на острове никого не
осталось. Сколько рыцарей было на острове сначала?
Варианты:
(A) 671 (Б) 1006 (В) 1007 (Г) 2012 (Д) 2013
29. В каждый из десяти кружков на рисунке требуется вписать по одному числу из набора 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 и 11 (каждое число можно использовать не больше одного раза). При этом на каждом из шести отрезков число, написанное в среднем кружке, должно равняться сумме чисел, написанных в крайних кружках. Какое из данных чисел не понадобится?
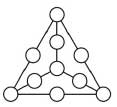
Варианты:
(A) 2 (Б) 4 (В) 6 (Г) 10 (Д) любое
30. Сколько существует 2013-значных чисел таких, что любое двузначное число, образованное парами соседних цифр, делится на 17 или на 23?
Варианты:
- 7 (Б) 9 (В) 13 (Г) 15 (Д) 3125
Ответы на конкурс «Кенгуру»-2013 для 5-6 класса:
1.Б
2.В
3.Д
4.А
5.В
6.Д
7.В
8.Г
9.В
10.Б
11.Г
12.Г
13.В
14.Д
15.В
16.А
17.В
18.Г
19.Б
20.А
21.Б
22.Г
23.Г
24.Д
25.Б
26.А
27.Б
28.В
29.Г
30.Б
Внимание
Объемная (3D) снежинка из бумаги
Написать письмо Деду Морозу!!!
Разносклоняемые существительные