Приближается международный математический конкурс «Кенгуру».
Предлагаем вам задания и ответы на «Кенгуру» для 9-10 классов 2011 года.
Ответы находятся внизу страницы, после заданий и перед комментариями.

Задачи, оцениваемые в 3 балла

1.         Электронные часы показывают время 20:11. Сколько минут пройдет прежде, чем часы впервые покажут тот же набор цифр 0, 1, 1 и 2 в некотором другом порядке?
Варианты:
(А) 49 (Б) 50  (В) 59  (Г) 60  (Д) 120

2.         На двух соседних сторонах правильного шестиугольника построили по квадрату. Чему равен угол a ?

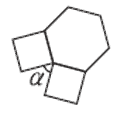
Варианты:
 (А) 40° (Б) 45° (В) 50° (Г) 60° (Д) 80°

3.         Какой ученый дал свое имя системе координат на плоскости?
Варианты:
 (А) Пифагор (Б) Евклид (В) Архимед (Г) Виет (Д) Декарт

4.         При сложении длин трех сторон некоторого прямоугольника получается либо 20, либо 22. Каков периметр этого прямоугольника?
Варианты:
 (А) 14            (Б) 18  (В) 28  (Г) 38  (Д) 56

5.         Жан-Кристоф продолжает изучать русский язык. Он записал цифрами и словами самое маленькое из натуральных чисел, для словесной записи которых требуется три слова. Какова сумма цифр этого числа?
Варианты:
 (А) 2  (Б) 3    (В) 4    (Г) 5    (Д)6

6.         На рисунке точки А и В — середины боковых сторон трапеции. Площадь закрашенного прямоугольника равна 13 см2. Какова площадь трапеции?

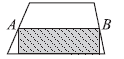
Варианты:
 (А) 27 см2 (Б) 26 см2 (В) 25 см2 (Г) 24 см2 (Д) невозможно определить
 

7.         Какое из неравенств А — Г обязательно верно, если а> 5 и а-b< 3?
Варианты:
 (A) b > 2 (Б) b < 2 (В) b < 8 (Г) b > 8
(Д) ни одно из неравенств А — Г не обязано выполняться

8. Жук ползает по клетчатой плоскости (сторона клетки равна 1 см). Он выполз из точки О, прополз вверх 1 см, потом вправо 2 см, потом опять повернул направо и прополз 3 см, потом — 4 см, и т. д. Сколько раз он был на расстоянии 2 см от точки О?

Варианты:
 (А)1 (Б) 2 (В) 3 (Г) 4 (Д)5

9. Чему равно отношение удвоенного квадрата утроенного куба ненулевого числа а к утроенному кубу удвоенного квадрата этого же числа?
Варианты:
(А) ¾   (Б) 4/3 (В)3/2 (Г) 9/2 (Д) ответ зависит от а

10. Из 18 одинаковых спичек сложили картинку, изображенную на рисунке. На ней имеется 13 треугольников. Какое наибольшее количество треугольников можно «разрушить», убрав всего одну спичку?

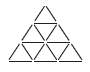
Варианты:
(А)1    (Б) 2  (В)3  (Г) 4 (Д) 5

 
Задачи, оцениваемые в 4 балла

11.      

12.       Если 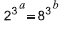, то обязательно
Варианты:
 (A)a=3b   (Б) а=b + 3  (В) a=4b  (Г) а = b + 1  (Д)b=a + 1

13.       Маленькая Яна схематично нарисовала карту своей деревни. Она изобразила 4 улицы (А, Б, В и Г) и отметила все 7 точек их пересечения. Однако в действительности ровно 3 из этих улиц являются прямыми. Какая из улиц не прямая?

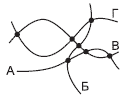
Варианты:
 (А) А (Б) Б    (В) В   (Г) Г
(Д) невозможно определить по этому рисунку

14.       Если отношение двух натуральных чисел равно 3:2, то отношение их наименьшего общего кратного к их наибольшему общему делителю равно
Варианты:
 (А) 1,5           (Б) 2    (В)3     (Г) 5    (Д)6
 

15.       Правильный треугольник и квадрат расположены так, что площадь их пересечения равна трети площади треугольника и одновременно четверти площади квадрата. Каково отношение сторон треугольника и квадрата?
Варианты:

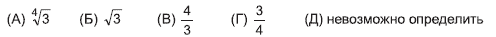
16. Каково наибольшее количество последовательных трехзначных чисел, каждое из которых имеет хотя бы одну нечетную цифру?
Варианты:
 (А) 1  (Б) 10  (В) 110           (Г) 111            (Д) 121

17.       Учитель задал на лето отличнику Пете и двоечнику Васе задачи, причем Васе — в 4 раза больше задач, чем Пете. После каникул оказалось, что Петя и Вася решили поровну задач, и процент задач, решенных Васей, равен проценту задач, не решенных Петей. Сколько процентов задач решил Петя?
Варианты:
 (А) 40% (Б) 50% (В) 60% (Г) 80%  (Д) 90%

18.       Пусть х> 1, у > 1. Какая из следующих дробей самая большая?
Варианты:

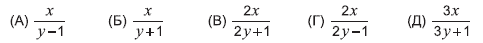
19.       Выделенные отрезки можно получить друг из друга поворотом вокруг некоторой точки. Какие из отмеченных точек могут быть центрами такого поворота?

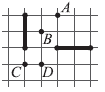
Варианты:
 (А) только А (Б) А и С (В) А и D (Г) только D (Д) В и D

20.       Марк выписал числа от 1 до 9 в некотором порядке. Затем он нашел среднее арифметическое в каждой паре соседних чисел в этом ряду и сложил получившиеся 8 чисел. Какая наибольшая сумма могла у него получиться?
Варианты:
 (А) 36,5 (Б) 43,5       (В) 45  (Г) 45,5           (Д) 90

Задачи, оцениваемые в 5 баллов

21.       Учитель сказал: «Вы, конечно же, не можете не знать, что квадрат нечетного числа не может быть четным числом». Что он имел в виду?
Варианты:
 (A)     Вы наверняка знаете, что квадрат нечетного числа может быть нечетным.
(Б) Вы, возможно, знаете, что квадрат нечетного числа всегда нечетен.
(B)       Вы, возможно, знаете, что квадрат нечетного числа всегда четен.
(Г) Вы наверняка знаете, что квадрат четного числа всегда четен.
(Д) Вы наверняка знаете, что квадрат нечетного числа всегда нечетен.

22.       Точка А с координатами (1,-10) лежит на левой ветви параболы у=х2 + bх+с. Какое из утверждений А — Г может быть неверным?
Варианты: 
(А) b< 0   (Б) b2 > 4c   (В)с< 0  (Г) b + c < 0   (Д) все утверждения А — Г обязательно верны
 

23. Две окружности расположены так, как показано на рисунке. Отрезок АВ— диаметр меньшей окружности, О — центр большей окружности. Радиус большей окружности равен 1. Какова площадь заштрихованной области?

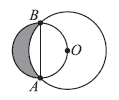
Варианты:

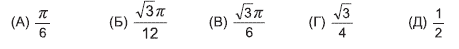
24.       В некотором месяце было 5 понедельников, 5 вторников и 5 сред. В предыдущем месяце было только 4 воскресенья. Тогда в следующем месяце будет
Варианты:
 (А) ровно 4 пятницы (В) ровно 4 субботы (В) 5 воскресений (Г) 5 сред       (Д) так не бывает

25.       На стороне ВС треугольника ABC выбрана точка D, а на отрезке AD выбрана точка Е. Найдите наименьшее возможное количество различных чисел среди величин углов, отмеченных цифрами 1,2 …. 9.

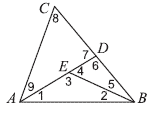
Варианты:
 (А) 1  (В) 2    (В)3     (Г) 4    (Д)5

26.       Из двух диаметрально противоположных точек кругового трека одновременно стартуют два велосипедиста. Они едут в одном направлении с постоянными скоростями. Время от времени первый велосипедист обгоняет второго. Восьмой обгон произошел через 1 час после начала движения. Через сколько минут после восьмого случится девятый обгон?
Варианты:
 (А) 4 (Б) 6 (В) 8 (Г) 10 (Д) невозможно определить

27.       Сколькими способами можно выбрать 4 ребра куба так, чтобы никакие два ребра из этой четверки не имели общих точек?
Варианты:
 (А) 6  (Б) 8    (В) 9    (Г) 12  (Д) 18

28.       В клетки таблицы 4x5 требуется вписать 20 различных натуральных чисел. Все числа должны не превосходить n, и для любых двух клеток, имеющих общую сторону, вписанные в них числа должны иметь общий делитель, больший 1. При каком наименьшем n это возможно?
Варианты:
 (А) 21            (Б) 24  (В) 25  (Г) 26  (Д) 27 (Д) невозможно определить

29.       Квадрат со стороной 1 разрезан на 4 треугольника одинаковой площади. Один из этих треугольников оказался остроугольным. Какова длина меньшей стороны этого треугольника?
Варианты:

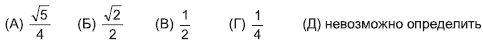
30. Среди попарных сумм некоторых 10 чисел не все целые. Какое наибольшее количество попарных сумм могут быть целыми?
Варианты:
 (А) 45            (Б) 40  (В) 36  (Г) 24  (Д) 10

Ответы:

1. (Б) 50
2. (Г) 60°
3. (Д) Декарт
4. (В) 28
5. (В) 4
6. (Б) 26 см2
7. (A) b > 2
8. (Г) 4
9. (А) ¾   
10. (Г) 4
11. (В) 40°
12. (Г) а = b + 1  
13. (В) В
14. (Д) 6
15. (A)
16. (Г) 111
17. (Г) 80%
18. (A)
19. (В) А и D
20. (Б) 43,5
21. (Д) Вы наверняка знаете, что квадрат нечетного числа всегда нечетен
22. (В)с< 0 
23. (Д) 1/2
24. (В) ровно 4 субботы
25. (В)3
26. (В) 8
27. (В) 9
28. (Г) 26
29. (A)
30. (В) 36

Внимание

Простая снежинка из бумаги

Объемная (3D) снежинка из бумаги

Написать письмо Деду Морозу!!!

Крыса из бумаги на 2020 год!

Разносклоняемые существительные