Завершился международный математический конкурс «Кенгуру»-2012. Представляем вниманию школьников 7-8 классов и их родителей возможность сверить свои задания с ответами к конкурсу «Кенгуру».
Вопросы сгруппированы по сложности (по баллам). Ответы на задания находятся после вопросов.

Задачи, оцениваемые в 3 балла

1.         Кенгуру способен прыгнуть в длину на 1 сантикилометр. Сколько метров составляет длина такого прыжка?
Варианты:
 (А) 1  (Б) 5    (В) 10  (Г) 50  (Д) 100

2.         Часы лежат на столе циферблатом вверх. Минутная стрелка сейчас указывает на северо-восток. Через сколько минут она укажет на северо-запад?
Варианты:
 (А) 45            (Б) 40  (В) 30  (Г) 20  (Д) 15

3.         В каком из следующих выражений при замене цифры восемь на любую другую цифру результат не изменится?
Варианты:
 (А) (8 + 8): 8 + 8
(Б) 8 • (8 + 8): 8
(В) 8+8-8+8
(Г) (8 + 8 - 8) • 8
(Д) (8 + 8 - 8): 8

4. Веня сложил лист бумаги пополам (как показано на рисунке) и сделал два прямых разреза ножницами. Затем он развернул лист. Какую фигуру он не мог при этом получить?

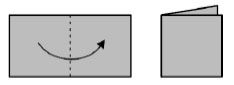
Варианты:

 
5. Натуральные числа х и у таковы, что 12х и 18y являются точными квадратами. Чему равно наименьшее возможное значение суммы х + у ?
Варианты:
 (А) 2  (Б) 5  (В) 7  (Г) 13  (Д) 30

 
6.         На рисунке изображена схема дорожек в парке. Каждая из этих девяти дорожек имеет длину 100 м. Аня хочет прогуляться из точки А в точку В, не проходя ни по какой дорожке дважды. Какова наибольшая длина такой прогулки?

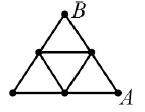
Варианты:
 (А) 900 м (Б) 800 м (В) 700 м (Г) 600 м (Д) 400 м

7.         Сколько существует различных треугольников, у которых одна из сторон равна 1, а два угла равны 50° и 60°?
Варианты:
 (А) 1  (Б) 2    (В) 3    (Г) 4    (Д) ни одного

8. Числа a, b, с и d таковы, что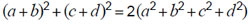
Тогда обязательно
Варианты:
 (А) а = с и b=d
 (Б) а = b и c = d
(В) a = d и b = c
(Г) a = b = c = d
 (Д) a+b = c + d
 

 
 
9. На какое наименьшее число треугольников можно разрезать фигурку кенгуру на рисунке?

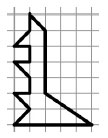
 Варианты:
 (А) 5  (Б) 6    (В) 7    (Г) 8    (Д)9

10. Чему равен куб периметра квадрата площади 4?
Варианты:
 (А) 4  (Б) 8    (В) 64  (Г) 512  (Д) 1024

 
Задачи, оцениваемые в 4 балла

11. Барбара заполняет пустые клетки таблицы (см. рисунок). Она хочет, чтобы сумма трех верхних чисел была равна 100, сумма трех средних чисел была равна 200, а сумма трех нижних чисел была равна 300. Какое число она должна поставить в среднюю клетку?

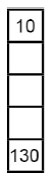
Варианты:
 (А) 50            (Б) 60  (В) 70  (Г) 75  (Д) 100

 
12.       Есть четыре карточки с надписями: «делится на 7», «простое», «нечетное» и «больше 100». На другой стороне карточек написаны числа 2, 5, 7 и 12. Для любой карточки число, написанное на ней, не обладает свойством, написанным на ее обороте. Какое число написано на карточке с надписью «делится на 7»?
Варианты:
 (А) 2 (Б) 5 (В) 7 (Г) 12 (Д) невозможно определить

13.       В пятиконечной звезде даны три угла (см. рисунок). Известно, что АВ=ВС. Чему равен угол х?

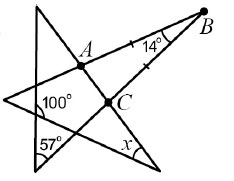
Варианты:
 (А) 35°  (Б) 42°  (В) 54°  (Г) 65°  (Д) 109°

14. Миша выбирает несколько чисел из набора 1, 2, ..., 10 так, чтобы ни одно выбранное число не было в два раза больше другого. Какова наибольшая возможная сумма таких чисел?
Варианты:
 (А) 37            (Б) 39  (В) 41  (Г) 42  (Д) 45

15. Число х положительно, а число у отрицательно. Что обязательно произойдет, если число х увеличится, а число у уменьшится?
Варианты:
 (А) х + у уменьшится
 (Б) xy увеличится
(В) x/y уменьшится
(Г) y/x  уменьшится
(Д) х-у увеличится

16. За один шаг робот может либо умножить данное число на 2, либо поделить его на 3, либо возвести его в квадрат. За какое наименьшее число шагов этот робот может превратить число 45 в число 200?
Варианты:
 (А) 7  (Б) 6  (В) 5  (Г) 4  (Д) 3

17.       Игральный кубик прокатили по клетчатой дорожке (см. рисунок). В каких двух позициях верхняя грань кубика была одна и та же?

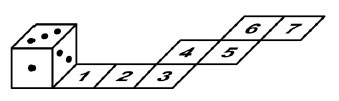
Варианты:
 (А) 1 и 7 (Б) 2 и 6 (В) 1 и 5 (Г) 2 и 7 (Д) 1 и 6

18.       У Пети и Коли были две одинаковые прямоугольные карточки. Каждый мальчик разрезал свою карточку на два прямоугольника. Сумма периметров прямоугольников, которые получились у Пети, равна 40, а у Коли — 50. Чему равен периметр исходной карточки?
Варианты:
 (А) 20  (Б) 24  (В) 30  (Г) 36  (Д) так разрезать карточки невозможно

19.       В одном городе 20% семей, имеющих кошек, имеют также и собак, 25% семей, имеющих собак, имеют также и кошек, а 20% всех семей не имеют ни кошек, ни собак. Сколько семей в этом городе имеют и кошек, и собак?
Варианты:
 (А) 50 %        (Б) 25 %          (В) 20 %         (Г) 10 %          (Д) 5 %

20. Какое число надо удалить из набора 1,2, 3, ..., 9, чтобы наименьшее общее кратное оставшихся чисел было самым маленьким из возможных?
Варианты:
 (А) 9  (Б) 8    (В) 7    (Г) 6    (Д) 5

Задачи, оцениваемые в 5 баллов

21.       Числа 1,2, ..., 12 расставлены по кругу так, что любые два соседних числа различаются либо на 2, либо на 3. Какие два числа стоят рядом?
Варианты:
 (А) 6 и 8        (Б) 3 и 5          (В) 7 и 9         (Г) 5 и 8
(Д) так расставить числа нельзя

22.       Все углы шестиугольника ABCDEF равны 120°. Известно, что АВ = 3, ВС = 4 , CD = 5 и EF=1. Найдите DE + AF.
Варианты:
 (А) 8  (Б) 10  (В) 13  (Г) 14  (Д) 15

23.       Натуральные числа а и b таковы, что a + b = 125. Какое из равенств А-Г возможно при некотором натуральном k ?
Варианты:

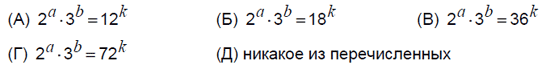
24.       В квадрате 3x3 расставлены числа так, что произведение чисел в каждой строке и в каждом столбце равно 1, а произведение чисел в каждом квадрате 2x2 равно 2. Какое число стоит в центральной клетке?
Варианты:
 (А) 16            (Б) 8   (В) 4    (Г)1/4  (Д)1/8

25.       Передние колеса роликовых коньков приходят в негодность после 300 км пробега, а задние — после 500 км. Диме подарили новые роликовые коньки. После скольких километров пробега ему нужно поменять местами задние и передние колеса, чтобы они прослужили одинаково долго?
Варианты:
 (А) 212,5 км (Б) 200 км (В) 187,5 км (Г) 175 км (Д) 162,5 км

26.       Равносторонний треугольник поворачивают относительно центра на 3°, потом на 9°, на 27°, и т.д. (на n-м шаге его поворачивают на 3ⁿ градусов). Сколько всего разных положений будет занимать треугольник?
Варианты:
 (А)3   (Б) 4    (В) 5    (Г) 6    (Д)360

27.       Произведение всех натуральных делителей числа n (включая и само n) оканчивается ровно на 15 нулей. На какое наибольшее количество нулей может оканчиваться число n ?
Варианты:
 (А) 5  (Б) 4    (В) 3    (Г) 2    (Д)1

28.       Бумажный прямоугольников CD со сторонами АВ = 3 и ВС = 9 перегнули так, что вершина С совпала с вершиной А (см. рисунок). Чему равна площадь закрашенного пятиугольника?

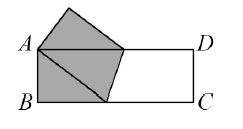
Варианты:
 (А) 18 (Б) 19,5 (В) 20,5 (Г) 21 (Д) 27

29.       Назовем семизначное число счастливым, если у него сумма цифр, стоящих на четных местах, равна сумме остальных цифр. Число может оказаться счастливым, если
Варианты:
 (A)     его цифры увеличиваются слева направо
(Б) его цифры уменьшаются слева направо
(B)       на всех нечетных местах стоит цифра 7
(Г) его средняя цифра равна 1, а остальные симметричны относительно нее
(Д) его средняя цифра равна 2, а остальные симметричны относительно нее
 

30.       У Васи много квадратов со стороной 1 и правильных пятиугольников со стороной 1. Он хочет сложить из них «кольцо», прикладывая имеющиеся многоугольники друг к другу сторонами так, чтобы квадраты и пятиугольники чередовались. При этом образовавшийся внутри кольца многоугольник должен быть выпуклым. Какое наименьшее количество фигур ему придется использовать?
Варианты:
 (А) 8  (Б) 10  (В) 12  (Г) 16  (Д) 20

Ответы к конкурсу «Кенгуру»-2012 для 7-8 класса:

1. В
2. А
3. Д
4. Г
5. Б
6. В
7. В
8. Б
9. Б
10. Г
11. Б
12. Б
13. В
14. Г
15. Д
16. В
17. Д
18. В
19. Г
20. В
21. А
22. Г
23. Г
24. А
25. В
26. Б
27. Г
28. Б
29. Д
30. В

Внимание

Простая снежинка из бумаги

Объемная (3D) снежинка из бумаги

Написать письмо Деду Морозу!!!

Крыса из бумаги на 2020 год!

Разносклоняемые существительные